Munkres-Algorithmus

Der Munkres-Algorithmus ist auch bekannt als Hungarian Method oder Linear Sum Assignment, ist ein Lösungsmethode für das Assignment Problem, welches dieses in Polynominalzeit lösen kann. Der Algorithmus ist elementar zur Minimierung von Fahrtzeiten, wenn mehrere Roboter auf verschiedene Positionen verteilt werden sollen, wie beispielsweise bei Einnahme der Startformation, oder bei dem Bauen von Mauern.

Ziel des Algorithmus

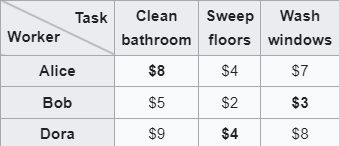
Die Aufgabe des Assignments Problems besteht darin, die optimale Zuweisung von Agenten zu unterschiedlichen Tasks zu finden. Dabei wird davon ausgegangen, dass jeder Agent für jeden Task unterschiedlich gut geeignet ist, diese Eignung wird durch Kosten ausgedrückt. Des Weiteren wird davon ausgegangen, dass jeder Agent genau einen Task übernimmt, keine Tasks von mehreren Agenten ausgeführt werden und die Anzahl an Tasks gleich der Anzahl an Agenten ist.

Das Problem soll im Folgenden Kurz anhand eines aus Wikipedia: Hungarian Algorithm entnommenen Beispiels demonstriert werden:

Alice, Bob und Dora sollen die Tasks Clean bathroom, Sweep floors und wash windows ausführen. Für jede dieser Aufgaben werden unterschiedliche Kosten definiert, wobei das Minimum dabei insgesamt 15€ sind. Besonders an diesem Fall ist auch, dass Bob für den Task Wash Windows zugeteilt wurde, obwohl die Kosten für Sweep Floors günstiger werden. Durch die Beschränkung, dass jeder Task nur von genau einer Person ausgeführt werden kann und darf, wird für diese einzelne Person jedoch eine nicht-ideale Zuordnung getroffen, um so die Gesamtkosten zu minimieren.

Implementation des Algorithmus

Für eine detailierte Betrachtung des Algorithmus lohnen sich verschiedene Blogs, wie z.B. hier:

• Brilliant: Hungarian Maximum Matching Algorithm
• Wikipedia: Hungarian Algorithm

Zur Implementierung sollten im Idealfall Bibliotheken verwendet werden, Scipy stellt im Rahmen des Optimize-Moduls hierfür Funktionen zur Verfügung:

• Scipy: Linear Sum Assignment

Die Bibliotheken verwenden im Allgemeinen NumPy Matrizen, um Daten effizient zu speichern und verarbeiten. Es können daher auch weitere Bibliotheken verwendet werden, um z.B. die Kostenmatrix zu erstellen, wie beispielsweise cdist von Scipy.

Anwendung auf Fußballrobotik

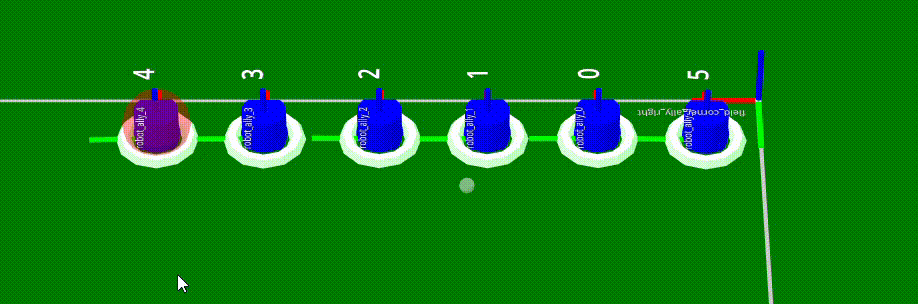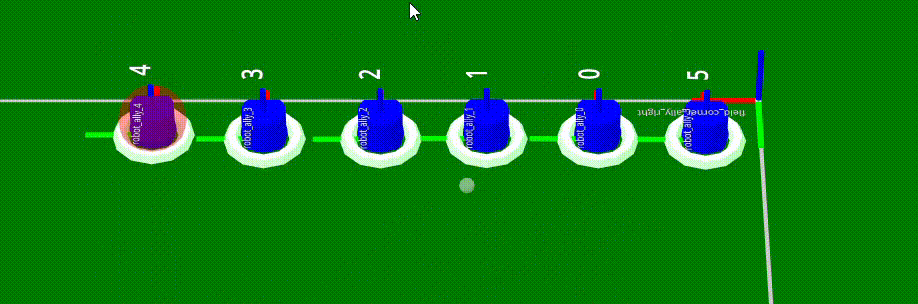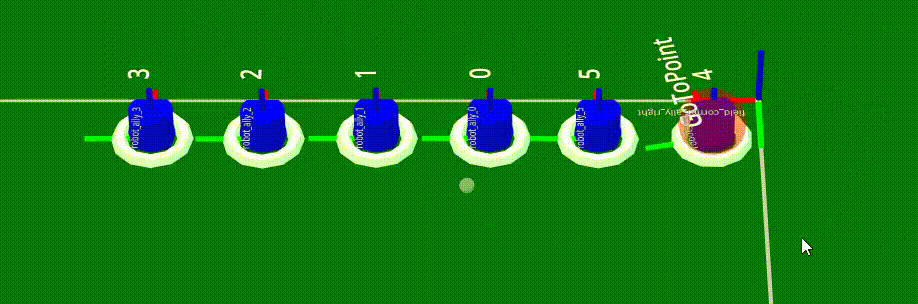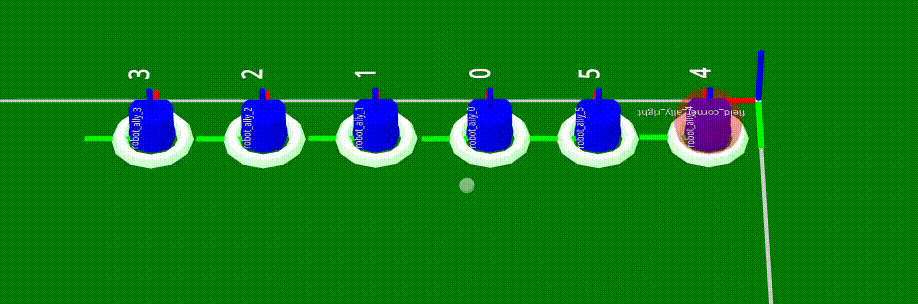
Der Munkres-Algorithmus ist zentral für die Zuordnung der Roboter zu unterschiedlichen Tasks. Die Roboter sind dabei die Agenten, die Tasks meist die Fahrt zu einer bestimmten Zielposition. Um die Kosten zu ermitteln, wird meist die Fahrtzeit oder Fahrtstrecke von der aktuellen Roboterposition zur Zielposition verwendet. Daher muss im ersten Schritt die Zielposition ermittelt oder geschätzt werden. Im Anschluss kann eine Matrix aufgestellt werden, die für jeden Roboter die Kosten für jeden Task beihaltet.
Die Wahl der Kostenfunktion ist dabei sehr wichtig, da sie das Verhalten der Roboter maßgeblich bestimmt. Im Allgemeinen sollten die Fahrtzeiten minimiert werden, diese sind durch die Beschleunigung, Pfadplanung etc jedoch schwer abschätzbar, weshalb sich die Strecke als praktikableres, wenn auch leicht schlechteres Maß anbietet.

• Euklidischer Abstand:
  Die Kosten werden durch den Abstand von der Start- zur Zielposition definiert, gemäß:
  c = sqrt((x1-x2)^2 + (y1-y2)^2)
  In diesem Fall werden alle Roboter mit derselben Priorität betrachtet. Dies bedeutet auch, dass Teams, die sich bereits an ihrer Zielposition befinden, oftmals auch an der Zielposition verbleiben, da das Verlassen dieser meist in höheren Kosten resultieren würde. Diese Funktion eignet sich, wenn Roboter allgemein an ihrer Position verbleiben sollten. Zwar ist die gesamte Fahrtzeit länger, werden z.B. beim decken von Gegnern diese nicht verlassen, wenn sich z.B. ein zu deckender Gegner ändert. Dies folgt somit dem "Einer für Alle"-Prinzip, wobei ein Roboter eine weite Strecke fährt, damit alle anderen an ihrer Position verbleiben können.
  

• Quadratischer Euklidischer Abstand:
  Dieser Fall ist ähnlich zu dem Euklidischen Abstand, nur dass die Kosten quadriert werden:
  c = (x1-x2)^2 + (y1-y2)^2
  Durch die Quadrierung werden weite Strecken besonders stark bestraft. Dies führt dazu, dass Roboter teils auch eine Position verlassen, um Platz für andere Roboter zu machen. Dadurch kann es unter Umständen dazu kommen, dass Gegner ungedeckt bleiben. Vorteilhaft ist jedoch, dass die Fahrt besser parallelisiert wird, da die minimierung der längsten Fahrtzeit priorisiert wird. Dieses Verhalten ist z.B. gut für Mauern, da Roboter nicht um die Mauer herumfahren müssen. Stattdessen rücken andere Roboter zur Seite, um Platz zu machen, wodurch dies auch als "Alle für Einen" aufgefasst werden kann.
  

• Weitere Kostenfunktionen:
  Je nach Anwendungen können auch weitere Kostenfunktionen eingeführt werden. In der Nähe des Strafraums könnte beispielsweise eine Manhatten-Distanz verwendet werden, die die rechteckige Fahrtplanung um den Strafraums berücksichtigt. Diese berechnet sich somit nach:
  c = abs(x1-x2 + y1-y2)
  Außerdem könnten auch Prioritäten in die Kosten miteingearbeitet werden. Dadurch werden Tasks bevorzugt, selbst wenn dadurch die Fahrtzeiten länger werden. Da die Zuordnung in diesem Fall schlechter nachvollziehbar ist, sind diese Fälle besonders ausgiebig zu testen.

Erweiterung für unbalanced-Fälle

Wie in der Problemstellung beschrieben, wird davon ausgegangen, dass die Anzahl der Agenten gleich der Anzahl der Tasks ist. Dies ist der Standardfall, welcher auch als balanced Assignment bezeichnet wird. Ist dies nicht der Fall, liegt ein unbalanced Assignment vor. Auch dies lässt sich mittels des Munkres Algorithmus lösen, welcher hierfür jedoch angepasst werden muss. Das Allgemeine Vorgehen ist dabei, die Matrix durch die Einführung von Dummy-Spalten bzw. -Zeilen auf eine quadratische Form zu erweitern. Die Dummy Werte werden alle mit 0 ausgefüllt und am Ende die Zuweisung zu diesen manuell verworfen.